第三章 浅层神经网络
作业
10. In the same network as the previous question, what are the dimensions of Z^[1] and A^[1]?
都是(4,m) 。可以做一个计算。我们知道Z=WX+b,权重矩阵W维度是(4,3),而X矩阵的维度应该是(3,m),故WX得到的维度就是(4,m),b的维度是(4,1),则(4,m)+(4,1)时,(4,1)会触发Python广播机制,从而最终得到的Z^ [1]是(4,m)的大小。A^ [1]=g(Z^ [1]),所以A^ [1]的维度和Z^ [1]的一样。都是(4,m)。
编程作业
DeepLearning.AI/DeepLearningAiWeek3.ipynb at main · liyouxia920/DeepLearning.AI · GitHub
第四章 深层神经网络
作业
5. Assume we store the values for n^[l] in an array called layers, as follows: layer_dims = [n_x, 4,3,2,1]. So layer 1 has four hidden units, layer 2 has 3 hidden units and so on. Which of the following for-loops will allow you to initialize the parameters for the model?
for(i in range(1, len(layer_dims))):
parameter[‘W’ + str(i)] = np.random.randn(layers[i], layers[i - 1])) * 0.01
parameter[‘b’ + str(i)] = np.random.randn(layers[i], 1) * 0.01需要注意的是randn不能写成rand!!np.random.randn()是生成标准状态分布,取值大多在-3~ +3之间,有负有正;而np.random.rand()则是生成0~1之间的随机均匀分布。
10. Whereas the previous question used a specific network, in the general case what is the dimension of W^[l], the weight matrix associated with layer l?
W[l]的维度是 (n[l],n[l−1])。
编程作业
DeepLearning.AI/DeepLearningAiWeek4_1.ipynb at main · liyouxia920/DeepLearning.AI · GitHub
DeepLearning.AI/DeepLearningAiWeek4_2.ipynb at main · liyouxia920/DeepLearning.AI · GitHub
矩阵维数
DNN结构:
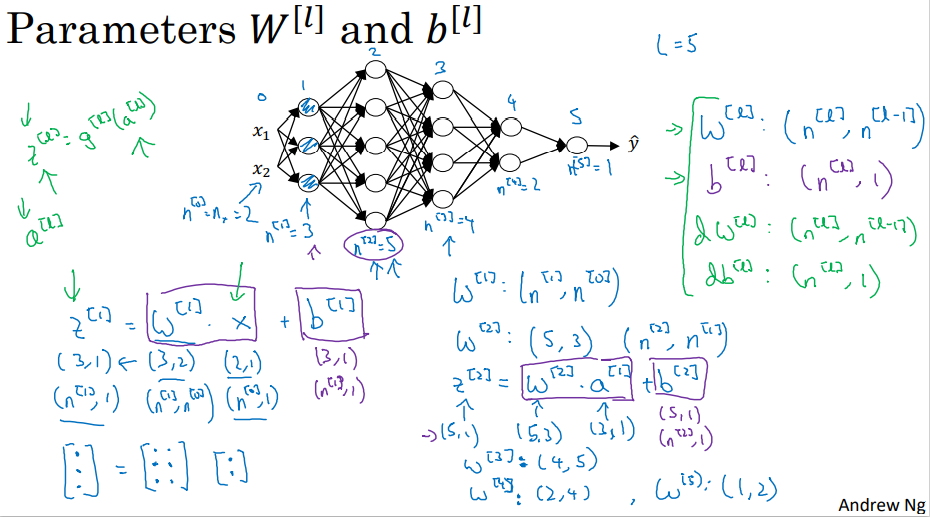
- 有一个隐藏层的神经网络,就是一个两层神经网络。
- 算神经网络的层数时,不算输入层,只算隐藏层和输出层。
正向和反向传播
正向传播
- input:
- output:
,
- 公式:
- 向量化:
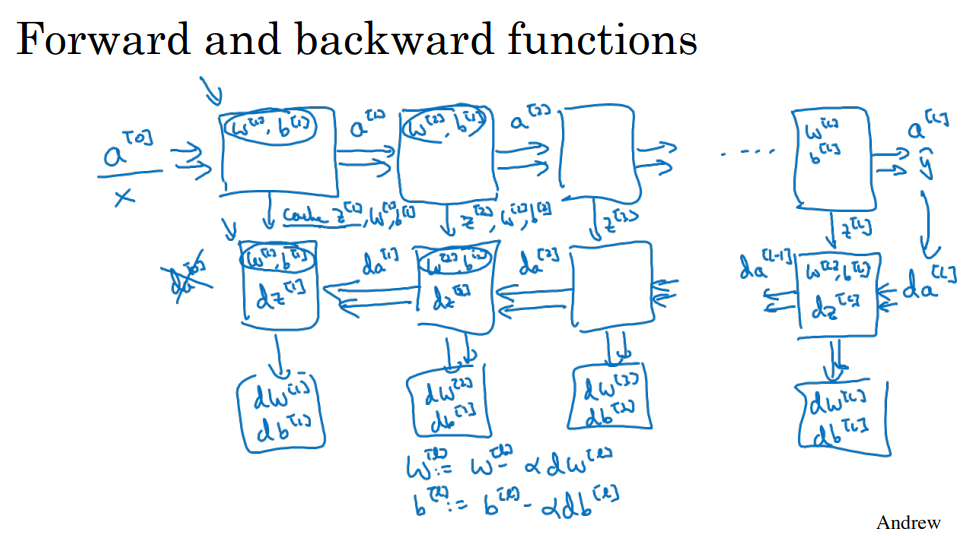
反向传播
- input:
- output:
,
,
- 公式:
将
代入
,有:
- 向量化:

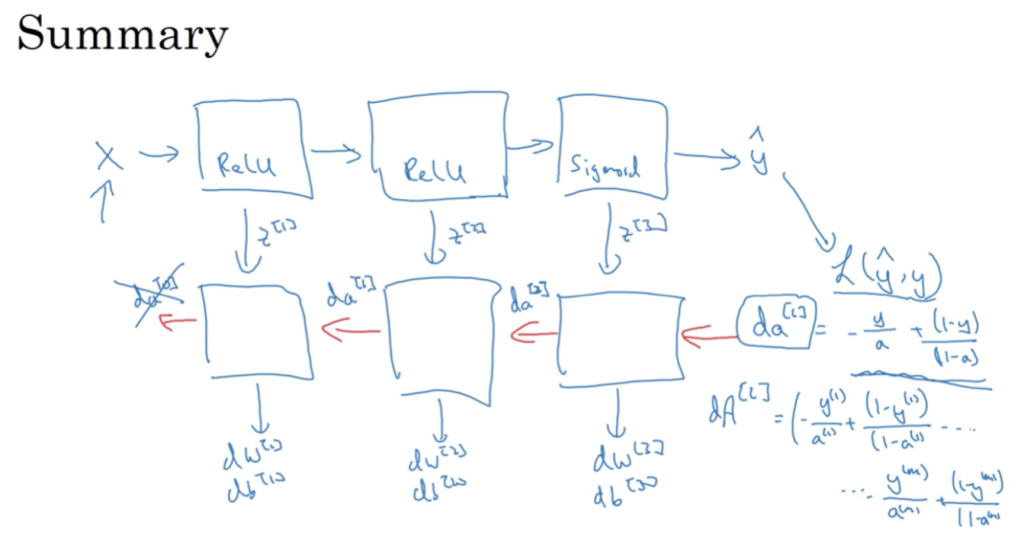
参数和超参数
参数:参数即是我们在过程中想要模型学习到的信息
超参数:超参数即为控制参数的输出值的一些网络信息,也就是超参数的改变会导致最终得到的参数 ,
的改变。
举例:
- 学习率 α
- 迭代次数 N
- 隐藏层的层数 L
- 每一层的神经元个数
- 激活函数 g(z) 的选择
通过Idea-Code-Experiment-Idea这个循环,尝试各种不同的参数实现模型,然后再迭代。
至此,第一门子课程《神经网络与深度学习》已结束。

