DeepLearning.AI – 第一周

2022年4月18日2022年4月18日作者 Li Youxia

2022年4月12日，我开始学习吴恩达的深度学习课程。

课程链接：

https://www.deeplearning.ai/program/deep-learning-specialization/ Coursera
DeepLearning.AI中国官网 – 深度学习专业 中国官网
https://www.bilibili.com/video/BV12E411a7Xn B站

参考习题：

参考笔记、课件

Welcome

本课程一共分为5门子课程：

神经网络与深度学习 (建立和训练神经网络)
改进深度神经网络 （Momentum和Adam算法)
构建机器学习项目 (端对端深度学习)
卷积神经网络 (CNN)
序列模型 (RNN, LSTM, NLP)

课程1：神经网络与深度学习

第一章：深度学习介绍

1. 什么是神经网络

ReLU激活函数 Rectified Linear Unit

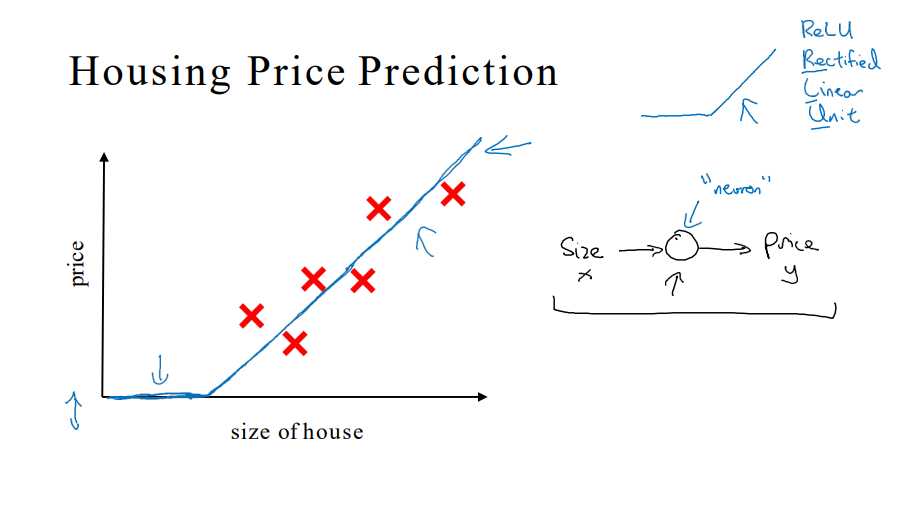
输入层x – 全连接的中间层 – 输出层y

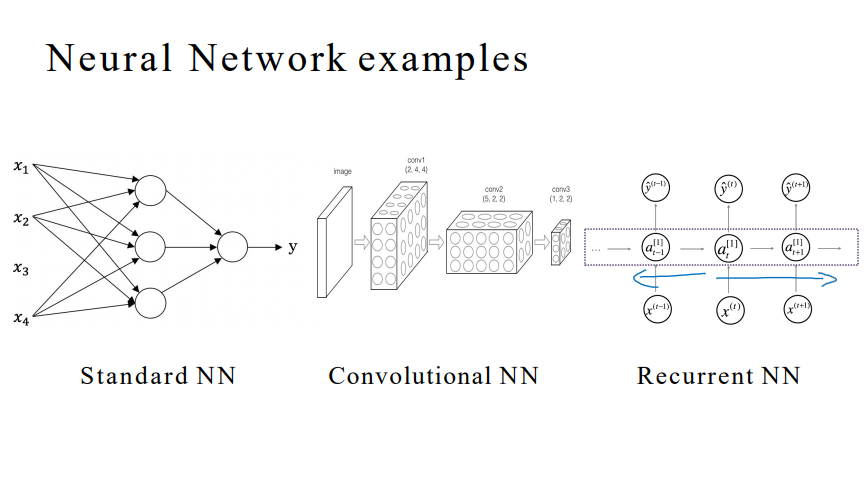
2. 监督学习与神经网络

监督学习
- 图像应用 – CNN
- 序列数据 – 音频/时间序列：RNN，语言：RNNs
- 自动驾驶 – 复杂混合结构

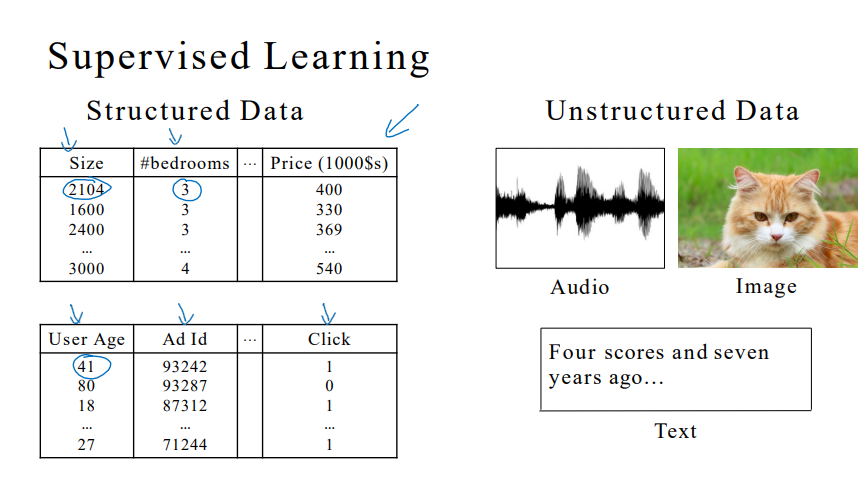
结构化数据和非结构化数据：找到应用点

3. 深度学习为什么兴起

更好的性能：要么训练一个更大的神经网络，要么投入更多的数据

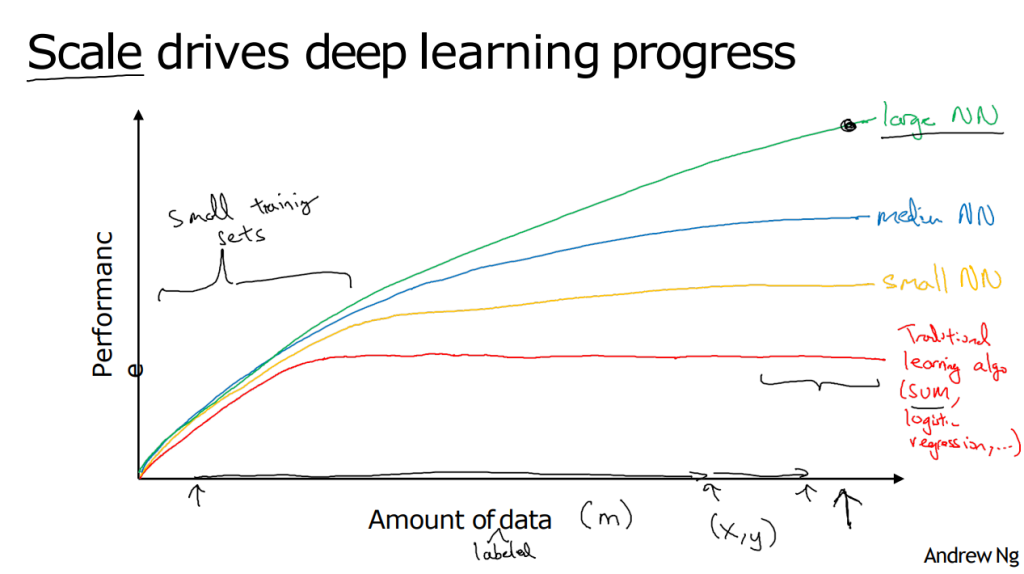
x轴是数据量，y轴是算法的性能
突破：从sigmoid函数转换到ReLU函数，使得梯度下降算法运行更快

4. 作业

为什么在上RNN（循环神经网络）可以应用机器翻译将英语翻译成法语？

【★】因为它可以被用做监督学习。
【  】严格意义上它比卷积神经网络（CNN）效果更好。
【★】它比较适合用于当输入/输出是一个序列的时候（例如：一个单词序列）
【  】RNNs代表递归过程：想法->编码->实验->想法->…

第二章：神经网络编程基础

逻辑回归作为神经网络

1. 二元分类

神经网络的训练过程可分为前向传播和反向传播
逻辑回归：一个二分类算法
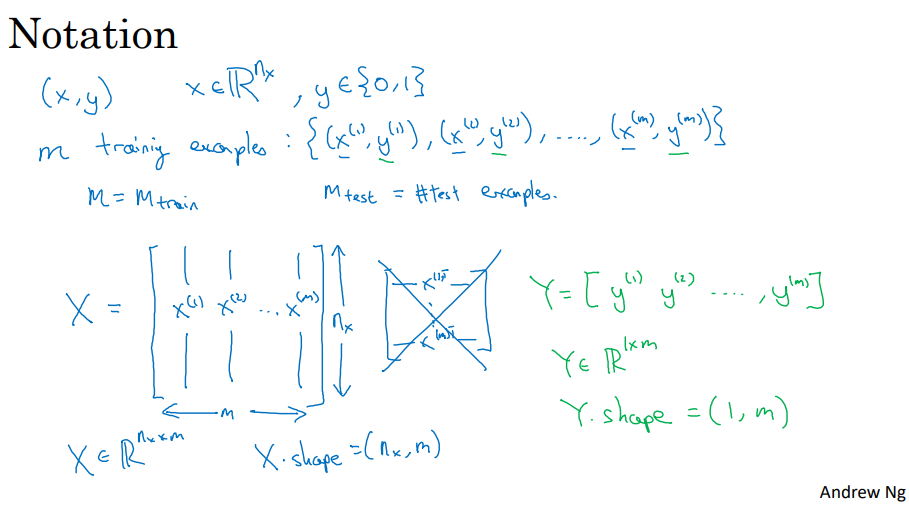
Notation:
- 样本：，训练样本包含个；
  - $x\in R^{n_{x}}$ ，表示样本 $x$ 包含 $n_{x}$ 个特征；
  - $y\in{0,1}$
训练数据： $\{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),\cdots,(x^{(m)},y^{(m)})\}$
输入神经网络时：
- 样本数据: $X.shape=(n_{x}, m)$
- 目标数据: $Y.shape=(1, m)$

2. 逻辑回归

sigmoid函数

3. 逻辑回归损失函数

损失函数 Loss function
- 为了得到全局最优解，选择凸函数
- $L(\hat y, y)=-(y\log\hat y+(1-y)\log(1-\hat y))$
代价函数 Cost function
- 是待求系数w和b的函数，优化w和b
- $J(w,b)=\dfrac{1}{m}\sum_{i=1}^{m}L(\hat y^{(i)}, y^{(i)})=-\dfrac{1}{m}\sum_{i=1}^{m}\left[y^{(i)}\log\hat y^{(i)}+(1-y^{(i)})\log(1-\hat y^{(i)})\right]$

4. 梯度下降法

通过损失函数界定模型对单一样本的训练效果
通过代价函数衡量参数w和b在设计的整个模型中的作用效果
每次迭代更新的修正表达式：
$w:=w-\alpha\dfrac{\partial J(w,b)}{\partial w}$ $b:=b-\alpha\dfrac{\partial J(w,b)}{\partial b}$
我们使用dw来表示 $\dfrac{\partial J(w,b)}{\partial w}$ ，用db来表示 $\dfrac{\partial J(w,b)}{\partial b}$ , α是学习率

5. 导数

通过斜率理解导数
- 斜率不变与斜率可变
- 复习求导公式

6. 计算图

正向传播和反向传播
- 流程图：从左到右，正向传播
- 导数：从右到左，反向传播

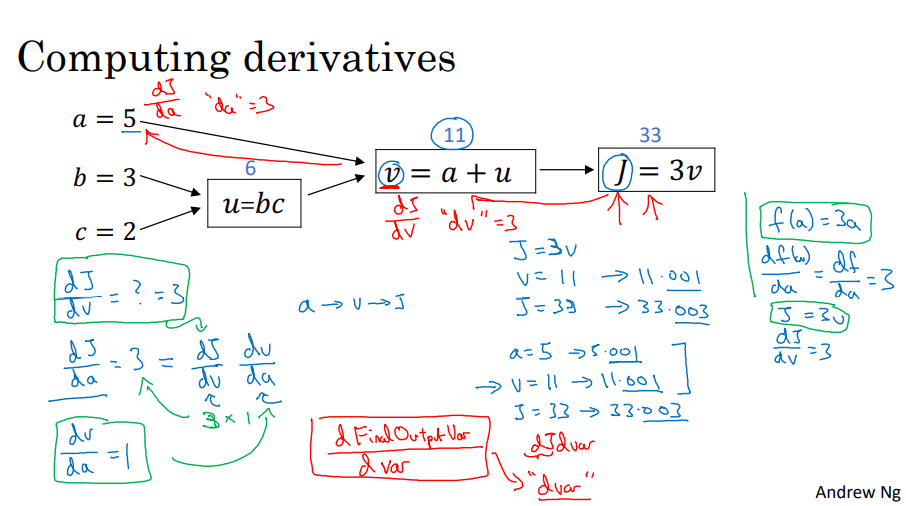
链式求导法则

7. 逻辑回归梯度下降

通过偏导数计算
$z= w^{T}x+b$ $\hat y=a=\sigma(z)$
损失函数： $L(a, y)=-(y\log (a)+(1-y)\log(1-a))$
反向传播过程：
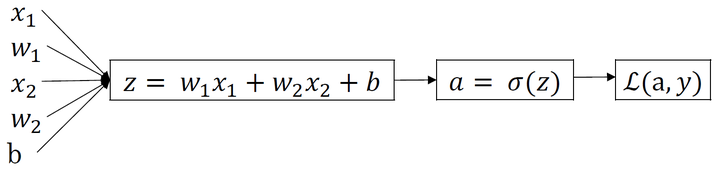
求da、dz：

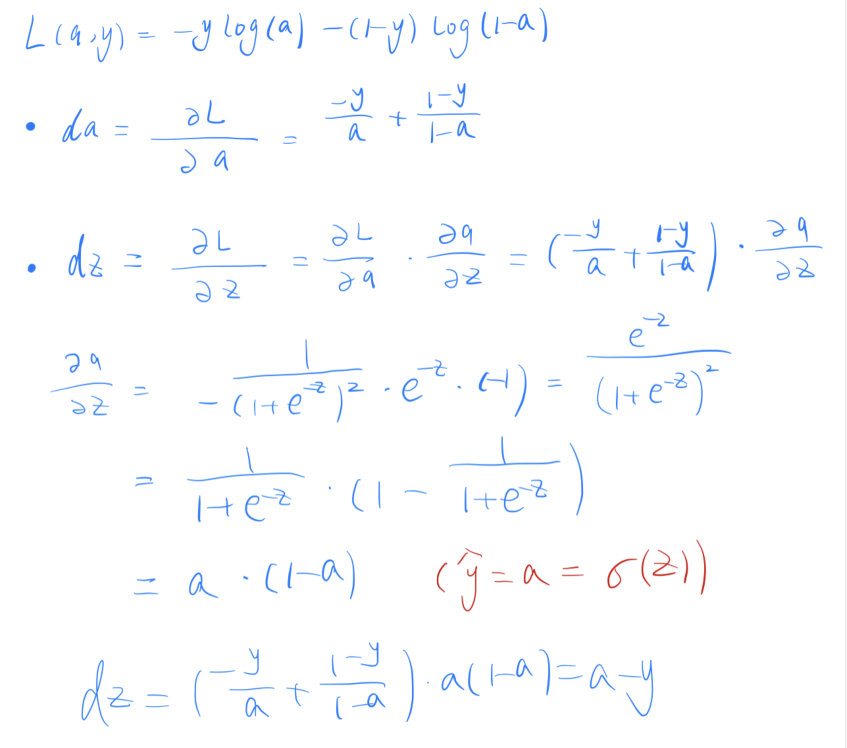
再对w1、w2和b进行求导：

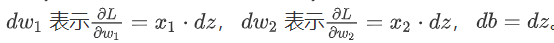
梯度下降法：

$w_{1}:=w_{1}-\alpha dw_{1}$ $w_{2}:=w_{2}-\alpha dw_{2}$

8. m示例上的梯度下降

通过向量化减少for循环，处理代价函数

Python和向量化

1. 向量化

摆脱显示循环，提高代码运行速度
理解前向传播和反向传播
使用numpy内置函数
单次迭代梯度下降

2. Python中的广播

axis = 0 表示垂直，axis = 1 表示水平
reshape 操作

3. Python/numpy向量的注释

避免使用秩为1的数组
积极使用n x 1 矩阵或者 1 x n矩阵，使用assert断言判断向量或数组的维度、reshape对数组设定所需的维度

4. 逻辑回归损失函数的解释

最大似然估计和独立同分布

发表评论取消回复