补充参考习题:
- GitHub – Kulbear/deep-learning-coursera: Deep Learning Specialization by Andrew Ng on Coursera.
- 0.0 目录-深度学习第四课《卷积神经网络》-Stanford吴恩达教授_Zhao-Jichao的博客-CSDN博客
- 吴恩达深度学习相关资源下载地址(蓝奏云)_何宽的博客-CSDN博客_蓝奏云学习资料合集
- 工作台 – Heywhale.com
笔记:大树先生的笔记
目录
第二章 神经网络编程基础
作业:
a = np.random.randn(4, 3) # a.shape = (4, 3)
b = np.random.randn(3, 2) # b.shape = (3, 2)
c = a*b //元素乘法需要两个矩阵之间的维数相同1. 请问数组c的维度是多少?
A. c.shape = (3, 3)
B. c.shape = (4,2)
C.计算无法发生,因为大小不匹配,会发生“错误”! D.c.shape = (4, 3)
2. 假设你的每一个实例有n_x个输入特征,想一下在X=[x^(1), x^ (2)…x^(m)]中,X的维度是多少?
A. (m,1)
B. (1,m)
C. (m,nx)
D. (nx,m)
编程练习:
第三章 浅层神经网络
1. 神经网络概览
[m]:第m层网络
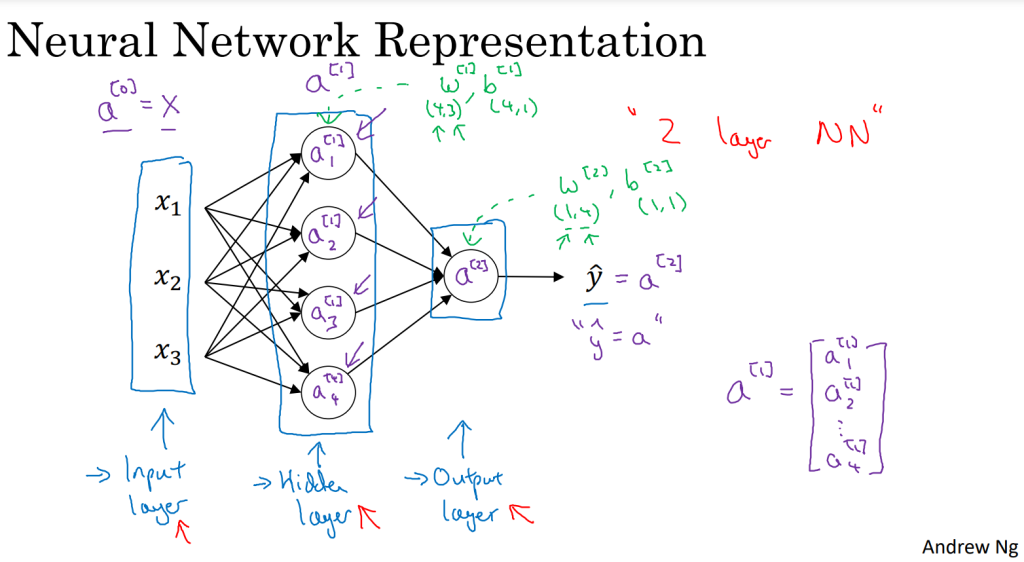
2. 神经网络的表现形式
- 输入层-隐藏层-输出层
- 通过带方括号上标的形式来指出这些值来自于哪一层
- 输入层和隐藏层之间
- w(4,3):4个隐藏层神经元,3个输入特征
- b(4,1)
- 隐藏层和输出层之间
- w(1,4):1个输出层神经元,4个隐藏层神经元
- b(1,1)
- 一个两层的神经网络示意图:
3. 计算神经网络的输出
- 每个结点都对应两部分的运算:z运算和a运算
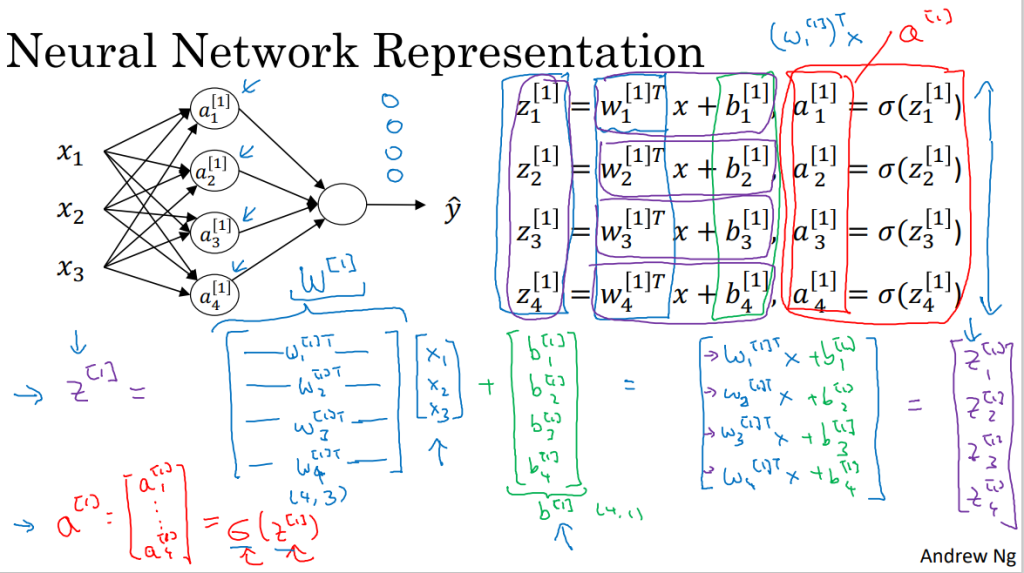
- 只需要用Python实现右边的四个公式即可实现神经网络的输出计算。要使用向量化计算。
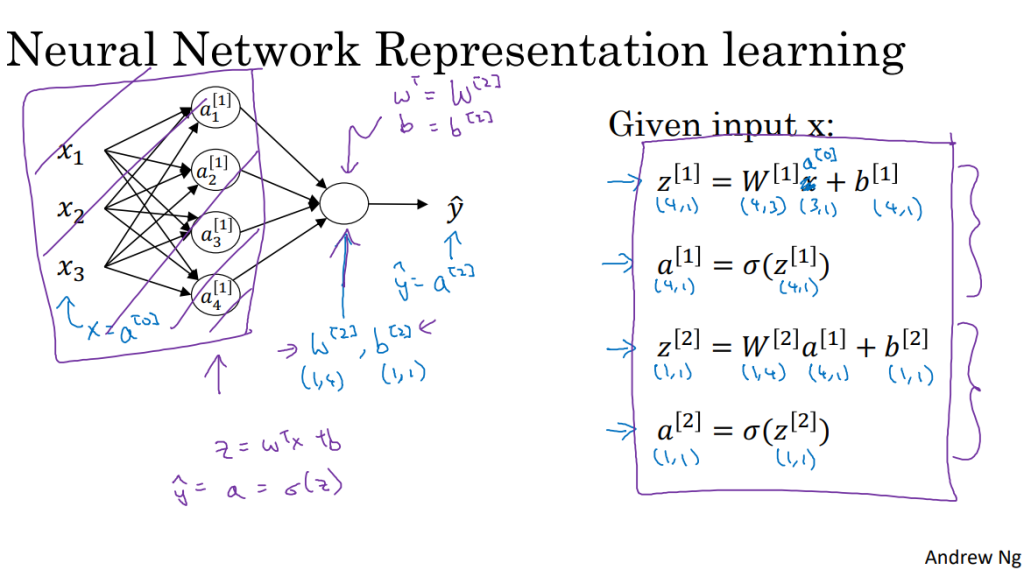
4. 多样本向量化
- 逻辑回归:将各个训练样本组合成矩阵,对矩阵的各列进行计算
- 神经网络:对逻辑回归中的等式简单地变形,让神经网络计算输出值

- 其实是把多个实例矢量化
- x -> X
- z -> Z
- a -> A
- 水平方向:training examples
- 垂直方向:hidden units

5. 向量化实现的解释
- 使用向量的方法(例子是四维向量),而不需要显式循环
- b -> Python 广播机制
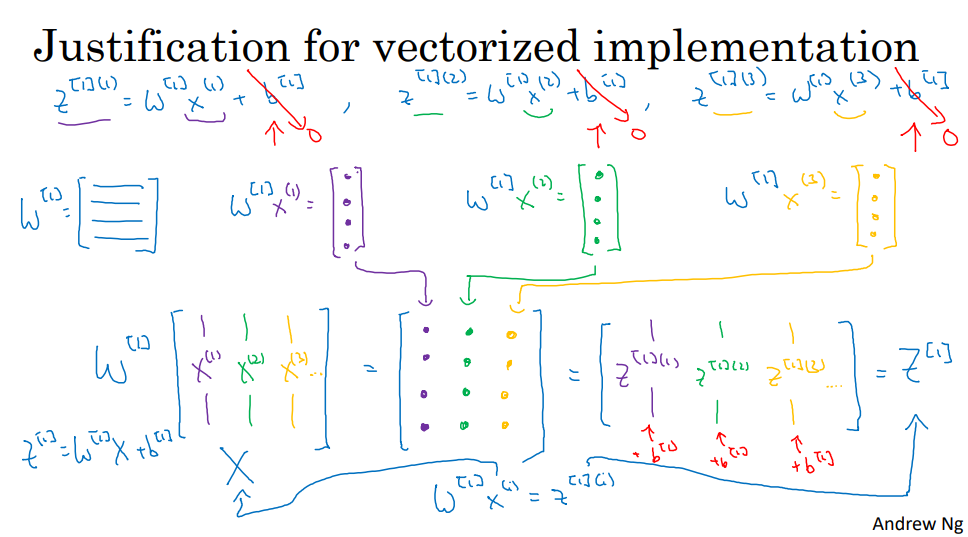
- 方程具有一定的对称性

- 仅使用sigmoid函数作为激活函数不是最好的选择
6. 激活函数
- tanh函数
- 二元分类时在输出层应该使用sigmoid函数
- 对函数斜率为0的影响最小
- ReLU(线性修正单元)函数
- leaky ReLU
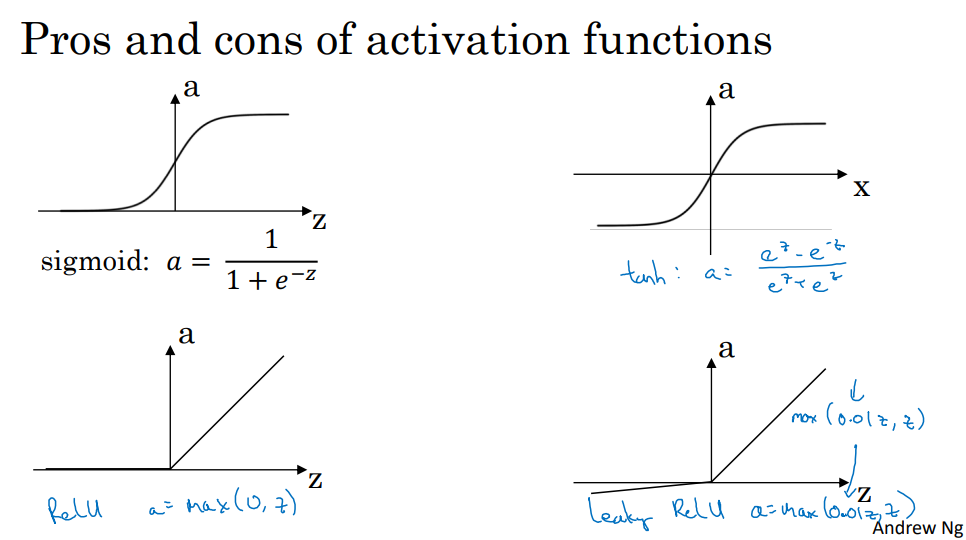
7. 为什么需要非线性激活函数
- 如果使用线性激活函数或者没有使用激活函数,无论神经网络有多少层,一直在做的只是计算线性函数,不如直接去掉全部隐藏层
- 所以,不能在隐藏层中用线性激活函数,可以用ReLU/tanh/leaky ReLU或者其他非线性激活函数
8. 激活函数的导数
- sigmoid函数
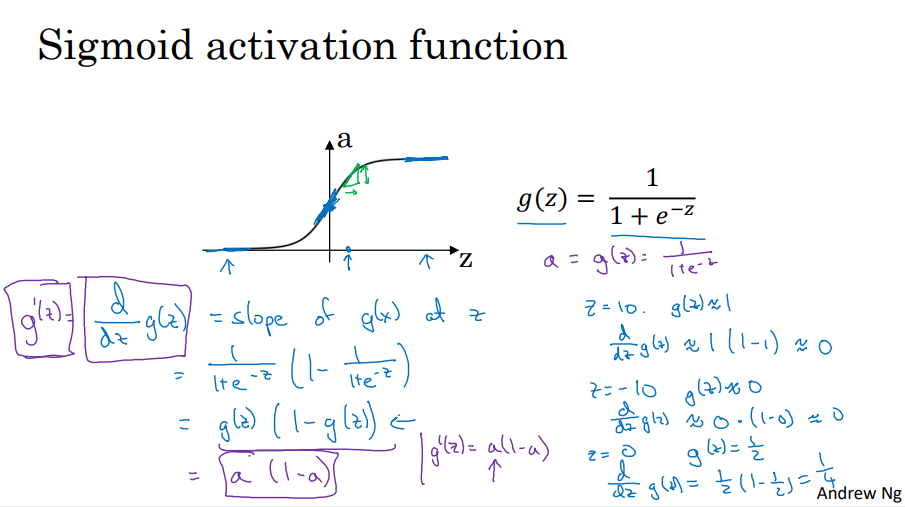
- tanh双曲正切函数
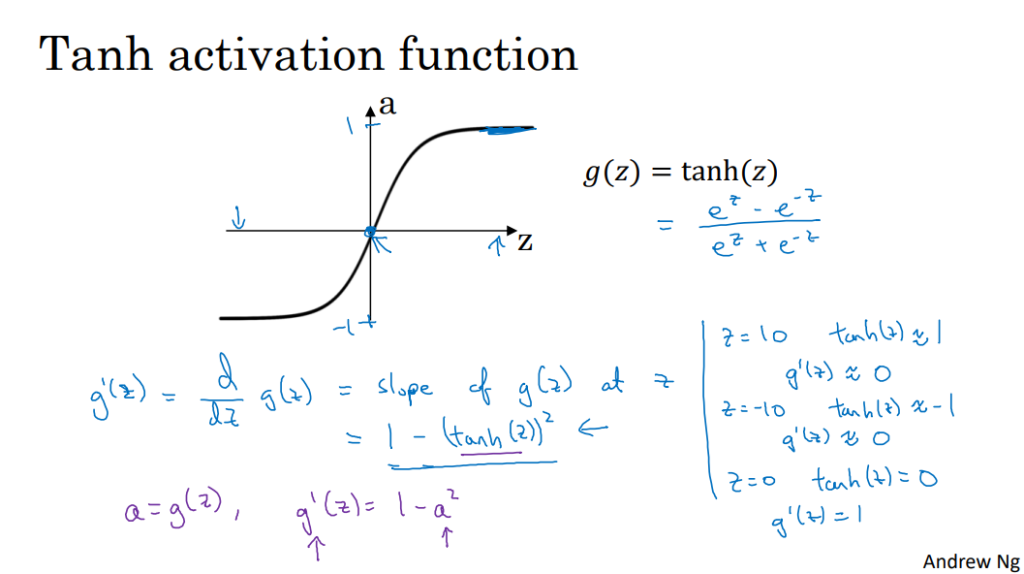
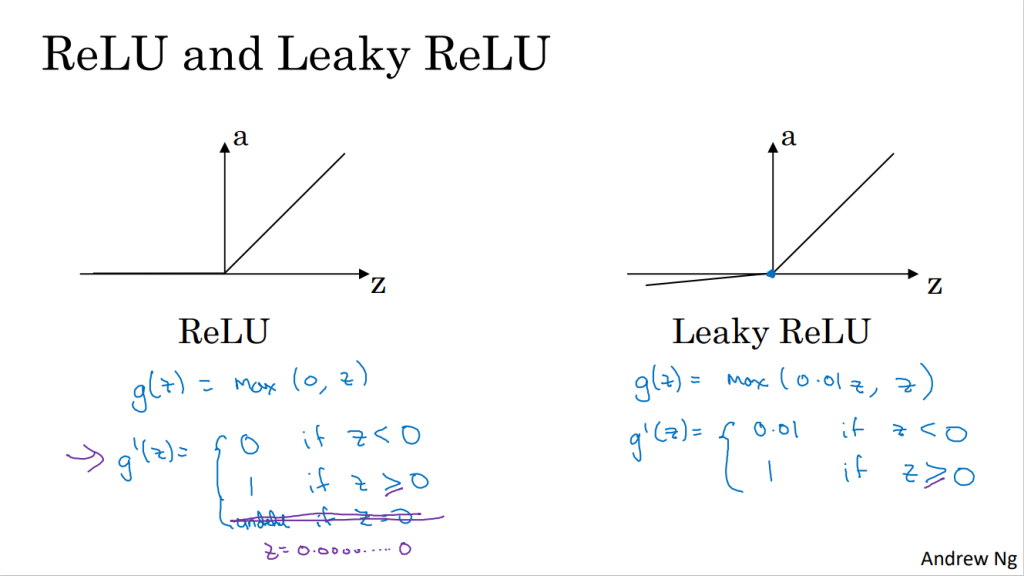
- ReLU函数和Leaky ReLU函数
9. 神经网络的梯度下降
- 以本节中的浅层神经网络为例,我们给出神经网络的梯度下降法的公式。
- 参数:
;
- 输入层特征向量个数:
;
- 隐藏层神经元个数:
;
- 输出层神经元个数:
;
的维度为
,
的维度为
的维度为
,
的维度为
- 参数:
- 前向传播的4个方程和反向传播的6个方程

- keepdims和reshape可以防止输出奇怪的秩数
10. 反向传播的直觉
- 线性代数对矩阵求导(链式法则):推导反向传播

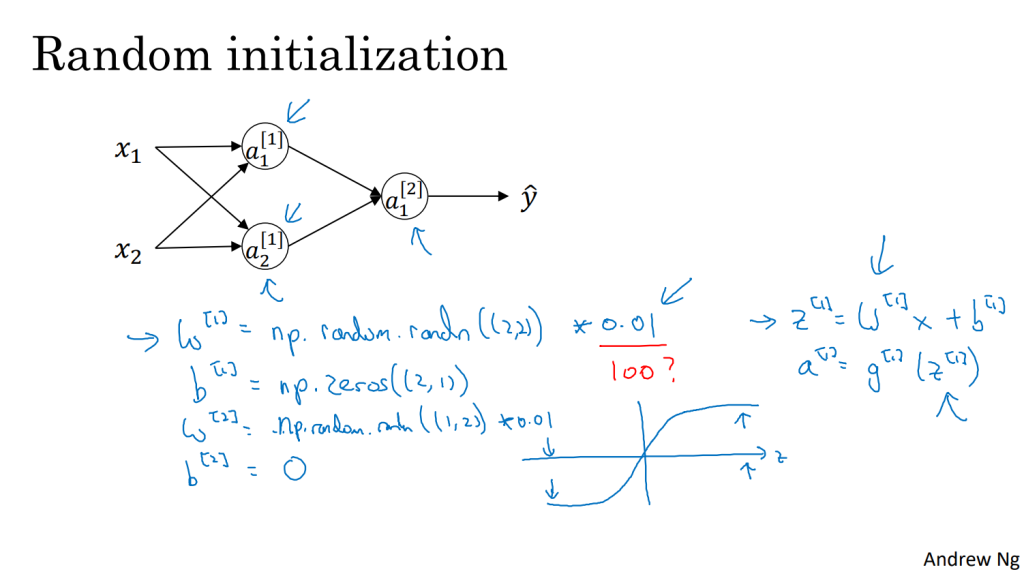
11. 随机初始化
- 对一个神经网络,如果权重或者参数初始化为0,梯度下降将不会起作用
- 初始化的例子:在初始化的时候,
参数要进行随机初始化,
则不存在对称性的问题它可以设置为0。 以2个输入,2个隐藏神经元为例:
W = np.random.rand((2,2))* 0.01
b = np.zero((2,1))- 使用很小的随机数以提高算法的更新速度